What is so *natural* about the natural logarithm?
I finally decided to dive deeper to dig out the germ of a question/source of confusion that I lazily acknowledged for almost a decade.
What is so *natural* about the natural logarithm?
If recap desired, see:
What is the logarithm?

- one can derive logarithms to any base, so then why choose the irrational number ‘\(e\)’ of value $2.71828$..? What made \(e\), a.k.a. Euler’s number, so special and how did it uniquely simplify calculations? Does the constant have a more tangible interpretation that I can understand?
- Did \(e\) derive its special position as the ubiquitous exponential function we use everywhere simply because of the nice properties the log to base e had? That is almost a cyclic argument, since the log was defined to be the inverse of the exponential function. There obviously was more, but…
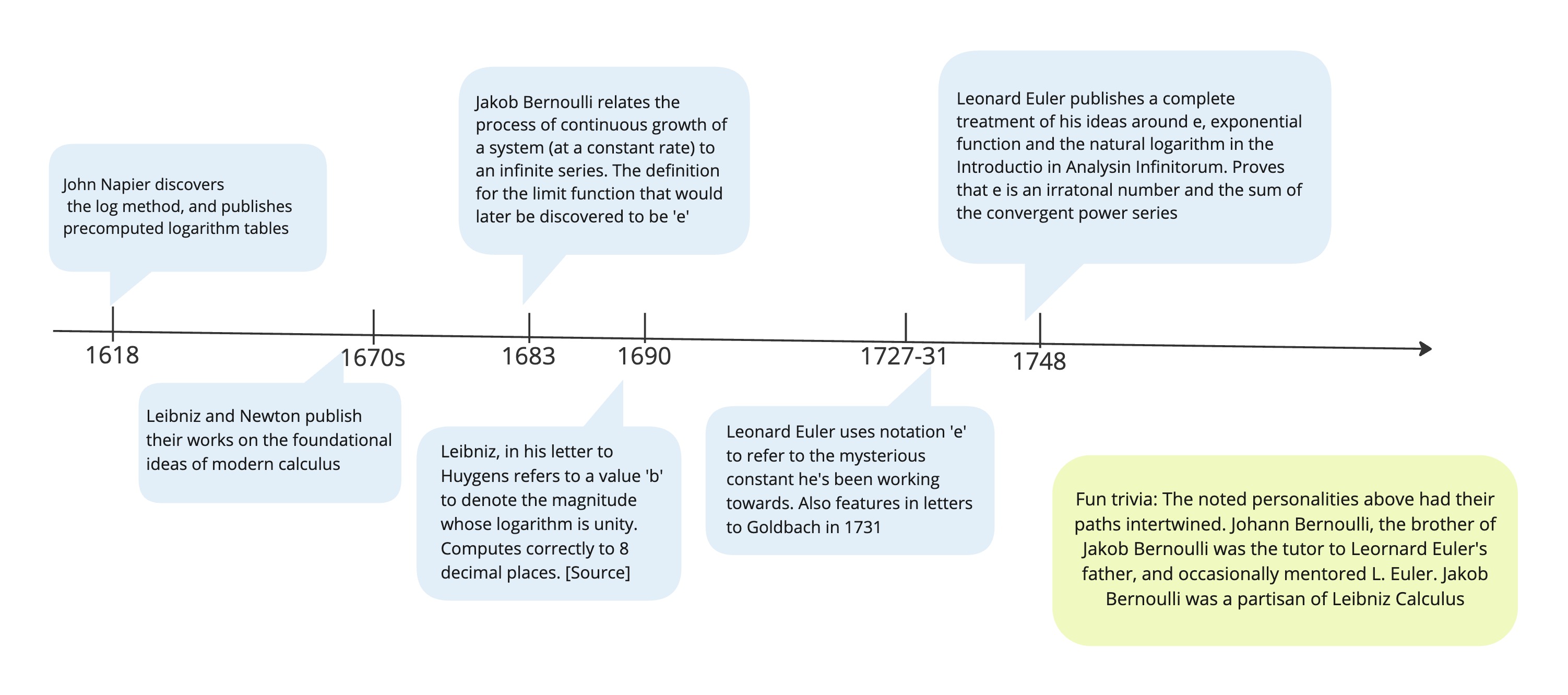
- My investigation began with how the mathematician (cum physicist cum astronomer) John Napier, discovered the logarithm and introduced the world to ‘logarithmic tables’ in $1614$. This was a numerical invention by Napier who was trying to simplify large, laborious calculations with big numbers that were commonplace in astronomy. I was amazed to learn that Napier had never explicitly arrived at or even recognised the presence of a foundational constant ($e$) underpinning his work. His logarithmic lookup tables predated the discovery of \(e\) and the tools of modern calculus. Yet, miraculously, the base used in his version of logarithms turned out to be a scaled version of \(e\): to be specific they involved the base \(\frac{1}{e}\) and the value $10^7$! The fact that \(e\), or some scaled version of it was the foundation of this entire table of hundreds of painstakingly computed numerical values, without any explicit knowledge or recognition of \(e\) had to be more than just coincidence. (Note, unlike Napier’s version above, modern day logarithms are calculated with the base ‘e’)
- One step further in my investigation, I revisited the contribution of the next popular character in the history of \(e\) - Bernoulli. Fascinatingly, according to math folklore, he inched closer to discovering this amazing number not through the lens of natural sciences or pure math, but from examining the financial concept of compound interest! He studied the question of how the growth of an initial principal amount of wealth would vary with different frequencies of compounding the interest. He demonstrated that as one continues to decrease the time period of compounding to an almost continuous scale, the rate of growth of the principal value increases at a decreasing rate, and converges to a ceiling value somewhere between $2.5$ and $3$. Spoiler: This was later found to be \(e\). What exactly did continually growing systems and natural logarithms have in common with each other?
Pulling the above thread organically lead me to a prism of questions (better late than never) about this beautiful mathematical constant \(e\) that seemed to underpin the structural definition of much of our mathematical world. I rediscovered an intuition for exponential and logarithmic functions, and how the constant \(e\) almost functioned as a wormhole, allowing us to cross over from one manifestation of a mathematical process, to its counterpart in seemingly different universes. For instance, \(e\) linked exponential functions, to infinite series, to the trigonometric universe, to symmetric or oscillating functions, to complex geometry, to explaining the evolution of systems, etc, which were in turn the tools that defined a good deal of physics. Along the way I had the revelation of how pivotal proving the irrationality of a number could be, and how this is linked to the convergence or divergence of an infinite series - something that had earlier never inspired me much.
These are age-old questions and undoubtedly, countless others have pondered and aha!-ed over them before. However,
I put on blinders (mostly) and went on a self-indulgent journey to chart this well-known terrain with curiosity as
a steer, only looking up online references for very specific technical obstacles. Since the path of reasoning I
followed was not always tuned to chronological events in history, a timeline of key events can be found in ‘
Timeline for select discoveries around \(e\)’.
Bernoulli and compound interest help approach \(e\)
Refresher - compound interest: Say an initial principal amount of money ($PV_0$) is invested at an annual interest of \(r=1\) an interest rate of $100\%$. If the interest is computed only once, at the end of the year, then the interest earned is $rPV_0$ or $PV_0$, and total money in the bank would become $(1+r)PV_0$, or $2PV_0$. Now, consider the scenario where instead of compounding the interest once a year, the bank calculated and attached it to the principal value twice a year, i.e., semi-annually. Then, the principal value at the end of 6 months grows to $(1+\frac{r}{2})PV_{0}$ or $(1.5)PV_0$, and after this sum is invested back, the final principal at the end of the year is equal to: $(1+r/2)(1+r/2) PV_0§§§§§$ or $2.25PV_0$. If the interest were compounded quarterly, then principal value at the end of the year would have grown to $(1+r/4)^4PV_0$ or $(1+0.25)^4PV_0$. In this manner we arrive at the general equation for the final principal value at the end of 1 year as or $(1+r/n)^nPV_0$ , where n is the number of times the interest is compounded during the year. At the end of t years is $(1+r/n)^{nt}PV_0$,
Bernoulli noted that as $n$ is continuously increased (i.e., the time period between successive interest calculations is shrunk), the resultant magnitude of principal value increases, but at a decreasing rate. If we wanted to compute what the principal value would be in the limit of $n->\infty$, i.e., under continuous compounding, we can do so by solving the general equation described above in the limit $n->\infty$. Making a base change of r/n-> 1/m, we get :
\[PV = \lim_{m->\infty} (1+\frac{1}{m})^{rm} *PV_{0}= \lim_{m->\infty}((1+\frac{1}{m})^m)^{r}*PV_0\] \[PV=(\lim_{m->\infty}(1+\frac{1}{m})^m)^{r}*PV_0\]Bernoulli thus showed that the effective growth factor for a series that was continuously compounded at a rate \(r\) was $(\lim_{m->\infty}(1+\frac{1}{m})^m)^{r}$. Whilst he did not solve this in the limit, he manually attempted to demonstrate that the infinite series $\lim_{m->\infty}(1+\frac{1}{m})^m$ converged to a number between 2.5 and 3 (around 2.7…. as per his calculations). Although Bernoulli is credited for defining the function that would in the future be known as \(e\), this limit was not solved until Euler nearly 50 years later.
Euler’s part of the puzzle
Leonard Euler rewrote the above infinite series $\lim_{m->\infty}(1+\frac{1}{m})^{m}$ to $\lim_{n->\infty}{1+1/n!}$ (Try this for yourself using the binomial theorem if you fancy). He then proved that infinite series was convergent and thus by definition the value of the sum of a convergent infinite series is irrational. Euler christened this irrational number as \(e\), and the notation has stuck.
Let that sink in. Without the pivotal proof of the irrationality of \(e\), we would not have a definite way to express
this naturally occurring constant that does not fit into our pre-defined conceptual number system of
finite (countable) quantities.
Evidence points to the fact that Euler recognised the significance of \(e\) late 1720s-early 1730s. However, it was only in 1748 that he published his work on \(e\), the exponential function, and the natural logarithm in his published work Introductio in Analysin Infinitorum [3].
Poetic epiphany
Let us plug this discovery back into the problem of compound interest, and see what it gets us:
\[PV_t = \lim_{n->\infty} (1+\frac{1}{n})^{nt} *PV_0\] \[PV_{t}=e^{rt}*PV_0\]In words, if $r=1.0$ (a 100% rate of interest), then in one year the growth in principal value ($\frac{PV_ {t=1}}{PV_0}$) will be $e$. At different $r$ and $t$ it will grow by $e^{rt}$.
One source by Jejus Nareja, sums the magnitude of this discovery so excellently that I will not attempt to rephrase. It gave me goosebumps.
"Just like every number can be considered a scaled version of 1 (the base unit) & every circle can be considered a
scaled version of the unit circle (radius 1), every rate of growth can be considered a scaled version of e (unit
growth, perfectly compounded). E is the base rate of growth shared by all continually growing processes; it shows up
whenever systems grow exponentially & continuously: population, radioactive decay, interest calculations, etc…
$$e$$ represents the idea that all continually growing systems are scaled versions of a common rate."
Some room for poetic personal epiphany: I realised on my bike ride to the grocery store, that it is the universality of a repeated action/process that births a constant. The action is constant. Here, the action of a quantity growing at a fixed rate is the constant that is being repeated, and its culmination (or repeated) is expressed as the constant \(e\). Not the other way round.
However, there were still missing parts to my original puzzle.
Faithful Calculus tells us why $e$ is special - derivatives deliver
I should have turned to calculus for the derivative (i.e., rate of change of \(e^x\) with respect to $x$)
earlier, but I always knew $\frac{\partial (e^x)}{\partial x}=e^x$ to be a fact. And that $\frac{\partial (a^x)}
{\partial x}$ was … oh wait, it was $a^{x}* log_{e(a)}$ and not $a^x$!
The fact that differentiating any other member of the family of general exponential functions other than when $a=e$ would result in its derivative being scaled by a factor of $log_ea$ seemed to hold the key to why $e$ was naturally special.
So, what did I re-realise?: (i) While all exponential functions ($a^{x,}a>0$) are special in that they have a rate of change proportional to themselves. This proportionality constant was $log_e(a)$, i.e., to a factor that is equal to the power \(e\) would have to be raised to, in order to equal \(\a\)!. It is only at the special value of $a=e$ that $log_e(e)=1$, making $\frac{\partial (e^x)}{\partial x}=e^x$. (ii) In fact, \(e^x\) is the only function to have both its derivative and integral equal to its own value. (iii) Any function that has its derivative proportional to the function itself (example, our friend - the function of growth for a principal value under compound interest), is of the form ($Ca^x, a>0$), and thus has its rate of change scaled by the constant $log_e (a)$. This presents the theoretical premise of the observation in previous sections that all continuous growth functions are scaled versions of a common rate, \(e\).
Was I now equipped enough to answer my original question? Not entirely. I did understand that any attempt to compute the pairs $a^x=y$ or $log_a(y)=x$ could always be intrinsically linked to the logarithm to the base \(e\). However, I was still searching for a pattern that would help anchor logarithmic tables of any base to the number \(e\). I still could not quite trace the contour of an exponential growth series, or an infinite series of the form ($\lim_{n->\infty}{\frac{1}{n!}}$), within the continual sea of numbers in a logarithmic table.
Timeline for select developments around \(e\)
Back to where it started: Napier’s logarithmic tables
So the Napier’s logarithm calculations have \(e\) hidden somewhere in plain sight. Where is it?
Let us understand how Napier motivated his invention of the logarithmic table in hope for some clues.
Napier was interested in finding ways to simplify the big multiplicative computations required in astronomy
at the time. Just as multiplication simplifies addition, and exponents simplify multiplication, Napier sought to
find the simplification for exponents.
The following description is excerpted from a lucid summary of John Napier’s method in ‘Logarithms: The Early History of a familiar function’ by the Mathematical Association of America: “Napier imagined two particles traveling along two parallel lines. The first line was of infinite length and the second of a fixed length (see Figures 2 and 3). Napier imagined the two particles to start from the same (horizontal) position at the same time with the same velocity. The first particle he set in uniform motion on the line of infinite length so that it covered equal distances in equal times. The second particle he set in motion on the finite line segment so that its velocity was proportional to the distance remaining from the particle to the fixed terminal point of the line segment.”

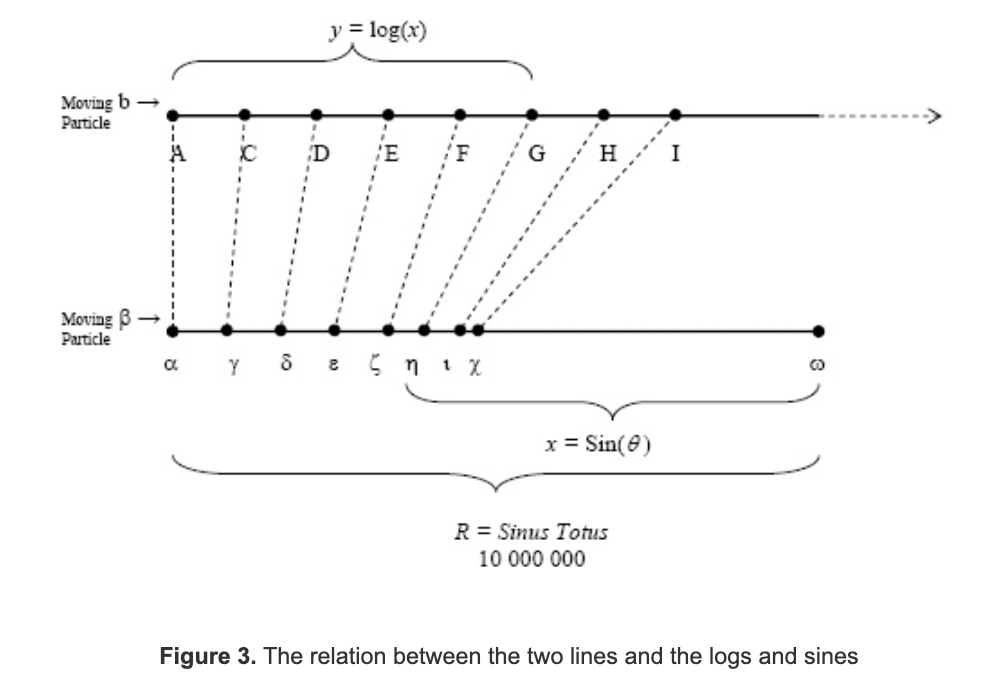
Napier then set about to show that the distance covered by a particle on the infinite line was the logarithm of the distance covered by the partnered particle on the finite line. He derived this based on trigonometric foundations. Details of proof are in [1]. However, this was not the most intuitive to me, and I tried to derive the relation between the distances traversed on both lines from a place of familiarity - the exponential functions.
Did I find the elusive connection to \(e\) in Napier’s work?
I was looking for the familiar continuous growth equations, or exponential functions in the above formulation.
Essentially, Napier wanted to find a method to go from a series of multiplication of numbers, to a corresponding space which transformed the task to a series of additions. What I found remarkable (not sure how necessary, though) was how Napier designed the thought experiment with kinematics to construct a coupled system between an arithmetic progression (distance covered of Particle A in Figure above) and a geometric progression (distance covered by Particle B). This emulated the relationship between logs and exponents that he desired.
Here are some personal deductions to supplement the proof that Napier offered in Figures 2, 3 above. The
first particle with uniform speed covers equal amounts of distance in equal amounts of time, and thus the distance traversed by it
has a linear and monotonic relationship in time. However, the second particle observes a decaying speed as it is
proportional to the particle’s distance to the terminal point, which decreases with time. Aha, now I spot the
exponential function!
The rate of change of distance (velocity) covered for the second particle is a continuously decaying function, with constant decay rate. If we study both particles for the same time durations of $\triangle{t}$, the first particle covers a distance that is linearly proportional to $\triangle{t}$. Thus over a series of $\triangle{t}s$, the distance covered by the first particle is an arithmetic progression in $\triangle{t}$. In the same $\triangle{t}$, the second particle covers a distance that is negatively proportional to itself($10^7-x$). Over the same series of $\triangle{t}s$, the second particle observes a continuously decaying growth in distance covered (I spy a geometric series, gasp!). In this manner, as one function (distance of Particle A) increases linearly at a constant rate, the other (distance of Particle B) increases at a decreasing rate, but proportional to itself. This resembled the properties you would expect from the relation between $log_e(x)$ to $e^{x}$. He in fact proved that if $x=sin\theta$, then $y=log_{nap}\theta$.
The second apple fell harder on my head when I realised why Napier’s log tables were to the base \(\frac{1}{e}\), and not \(e\). By virtue of Napier tying his proof to a continuously decaying function with a negative growth rate instead of a positive one, his calculations were centered around the base $\frac{1}{e}$ like so: For all $x<10^7$, the speed of particle B is a function of ($10^7-x$). Thus, $\frac {\partial x} {\partial t} = f(10^7-x)$ => $x = e^{f (10^7-x)}$ or $Ce^{-kx}$, where $C=e^{g(10^7)}$). Now, $y = (log_e(e^{-kx}) + log_eC) \propto (-kx)log_{e}(e)$ or $kx*(log_e(\frac{1} {e}))$. And lo, there is the $\frac{1}{e}$!
Finally, the answer to the question of ‘Why the original version of Napier’s log table had e as a pivotal element without intending to’ felt more in my grasp. All the puzzle pieces fit: (1) all continuous growth and decay processes have a growth rate that is scaled by e. (2) Taking the derivatives of the family of exponential functions $a^x$ beautifully demonstrates this. (3) Here in Napier’s kinematic experiment too, we recognise the same function patterns at play. (4) Further, because Napier chose to ground his framework with a decaying velocity of particle B (which was a direct consequence of the second line being of finite length), it naturally leads us to his logarithms being grounded to the base \(\frac{1}{e}\) instead of \(e\). Had the velocity of Particle B somehow been increasing, and not decreasing (continuous decay), the relationship would have had been a scaled factor of \(e\) instead of \(\frac{1}{e}\).
Closing - Hyping \(e\) as an anchoring lens to view world
Chief insight: Any process or system in physical and mathematical world that grows (decays) continuously is an exponential process, and all such processes have a growth rate that can be expressed as a scaled version of \(e\).
Rejuvenated world view, much? Currently, in my daily work in the field of Machine Learning applications, whenever I saw a scaling factor of $log_e(x)$ or \(e^x\) in the past week, it felt like I was recognising hidden morse code. One can look at a distribution and intuitively understand when they should choose a different function to fit or describe some aspect of the data. Reminded me of the ‘why’ behind ‘let’s use this’, beyond the argument ‘it gives the function/curve nice properties’.
With my newfound understanding of ‘\(e\)’ and the exponential function, I feel closer to finally, truly understanding complex geometry too (:P)
Bonus: here is a fun post that documents various puzzles and real world scenarios to show how the ‘transcendental constant \(e\)’ helps articulate the language of probability.
References
- Logarithms: The Early History of a familiar function Source
- History of Euler’s Numbers Source
- The Leibniz catenary and approximation of \(e\) an analysis of his unpublished calculations Source
- Derivative of \(e^x\) by Khan Academy Source
- Derivative of Log(x) (Slick Proof) Source
- Why \(e\), the Transcendental Math Constant, Is Just the Best Source